路径规划算法学习
路径规划:
蚁群算法:
信息素浓度函数是一个全局特征,它是之前的蚂蚁给当前蚂蚁的经验;启发函数是一个局部特征,它是当前蚂蚁在当前城市前往可前往城市最短距离的一个预计
其中Q是一只蚂蚁携带的信息素总量,Lk是第k只蚂蚁从城市i走到城市j的长度,于是信息素浓度函数就是蚂蚁在路径上释放信息素的浓度,表征了该蚂蚁对该路径长度的测定。
动态规划算法:
采用逆向寻优的思路,其基本思路是将路径分为若干个阶段,离起点或是终点距离相同的中间点为同一阶段。对于每一个阶段的每一个点,都找出该点前往下一个阶段的最优路径(指到达终点距离最近);如此这般,当逆推到上一个阶段的任意点经过该点到达终点的局部最优路径必定是该点的最优路径+任意点到该点的距离,而上一阶段某一点到达该阶段的最优路径必然是上一阶这点到达该阶段任意点的这些局部最优路径的最小值,逆推回起点确定了每一阶段前往下一阶段的最优路径后,从起点沿最优路径顺推回终点即为全过程的最优路径,这是一个很典型的最优化原理方法,以下面这个问题为例:
阶段4:从D1到阶段5的最优路径是5,D2到阶段5的最优路径是2
阶段3:从C1到阶段5的最优路径是C1->P5=min{C1->D1->P5,C1->D2->P5}=8
从C2到阶段5的最优路径是C2->P5=min{C2->D1->P5,C2->D2->P5}=7
从C3到阶段5的最优路径是C3->P5=min{C3->D1->P5,C3->D2->P5}=12
阶段2:从B1到阶段5的最优路径是B1->P5=min{B1->C1->P5,B1->C2->P5,B1->C3->P5}=20
从B2到阶段5的最优路径是B2->P5=min{B2->C1->P5,B2->C2->P5,B2->C3->P5}=14
从B3到阶段5的最优路径是B3->P5=min{B3->C1->P5,B3->C2->P5,B3->C3->P5}=19
阶段1:从A1到阶段5的最优路径是A1->P5=min{A1->B1->P5,A1->B2->P5,A1->B3->P5}=19
纵观这一算法,我们发现动态规划算法本质涉及了三层循环,最外层是阶段的逆向循环,中间层是当前阶段下各点的遍历循环,最里层是当前点前往下一阶段的任意点的遍历循环。在最里层循环结束后,我们得到了当前点前往终点的局部最优路径;在中间层循环结束后,我们得到了当前阶段每个点前往终点的局部最优路径,这将为最外层的下一次循环(进入上一阶段寻找局部最优路径)提供指导;在最外层循环结束后,我们便得到了一条最优路径。动态规划算法是从局部最优推导全局最优的算法,不需要存储全局的大量信息,而只需要告知局部的一个最优解。
RRT算法:
所谓目标区域,一般是Xnew和Xgoal之间的距离小于StepSize时,此时直接将Xnew和Xgoal相连便可得到最后的路径。
启发技巧:为了加速随机过程,可以让生成随机点Xrand时以一个相对于其他点较大的概率生成终点(5%-10%),这将有利于加速随机树向终点的生长过程。
RRT算法的优点是快,缺点是轨迹完全随机而仅仅为可行解,且有可能出现长时间迭代而找不到的情况,因而建议设置最大迭代次数避免浪费资源。
相比之下,RRT 算法在RRT算法的基础上增加了两步:重写和随机重连。
RRT 算法考虑每一个节点到出发点的距离,为此每一个节点会增加一个属性:到出发点的距离。相应地在每一个节点选择父节点的时候,新节点的距离等于父节点的距离加上父节点到子节点的距离。
重写就是在新节点Xnew加入到树种之后,重新为它选择父节点,好让它到起始点的路径长度(代价)更小。基本流程是:遍历整个树,获得到新节点Xnew的距离小于一定阈值(比如1.5倍的步长)的所有节点,将这些节点加入到一个列表中。
找到节点列表中具有最小距离的那个节点,将新节点Xnew的父节点设置为该节点。
随机重连就是在重写完成之后,对新节点Xnew附近一定范围内(可以与重写范围不同)的节点进行重连。重连就是,检查一下如果把Xnew附近的这些节点的父节点设置为Xnew,这些节点的代价会不会减小。如果能够减小,就把这些节点的父节点更改为Xnew;否则,就不更改。
RRT算法得到的轨迹是一个渐进最优的轨迹,如果单次调用,则它整体比RRT算法得到的轨迹都要更优,而如果循环迭代多次,则RRT算法将会得到一个趋近于最优的轨迹。
在RRT算法的基础上,我们进一步引出Informed RRT算法。
在RRT算法中,对于Xnew的选取仍然是近似于全局随机的,然而事实上,如果我们得到了一条通路,那么Xnew的选取优化就理应位于这条通路附近,Informed RRT算法提出:
当我们得出任意一条通路时,设Xstart与Xgoal的直线距离为Cmin,目前得到所有通路的长度最短值为Cbest,则可以将采样空间缩减为一个以Xstart与Xgoal为焦点,Cmin为焦距,Cbest为长径的椭圆(对于三维空间则为椭球),以此类推迭代。这么做相比RRT*算法可以大大减少迭代到渐进最优路径的时间。
遗传算法:模拟生物进化过程,适者生存
在轨迹优化问题中,生物个体就是每个不同的轨迹,我们通过一定的进化规则来找到在当前环境下最适合生存的个体(路径最短的轨迹)
由于轨迹从起点到终点必然经过方格的所有行和所有列,于是在轨迹初始化生成时要求每行都任选一个非障碍栅格,接下来判断相邻行的选中栅格之间是否连续(相邻或对角,对应栅格的x,y分量绝对值不大于1),不连续时则将选中栅格向下取平均插入新的栅格,如果该栅格为障碍栅格或已遍历栅格,则寻找其四周非障碍非已遍历栅格插入,如果无法找到则舍去此路径,重复这一过程直到轨迹连续,从而完成了一条轨迹的初始化。
多次进行轨迹生成,以此形成一个轨迹种群来进行遗传算法的循环。
轨迹规划:
人工势场法:
如此规定人工势场会带来两个问题:目标不可达和陷入局部最优。
为了解决这两个问题,我们可以改进斥力势场,让它在对障碍物表现斥力的同时额外还向目标点表现引力(似乎也不能完全解决问题?)
曲线插值法:
将轨迹规划为一条x,y分量均为与t相关的多项式曲线,则此时给出多项式与任意时刻,则在该时刻车的位置,速度,加速度和加加速度便被同时完全确定了。
对于位置、速度、加速度、加加速度的规划要求越高的,越是需要更高阶的多项式曲线。
位置多项式分横向和纵向两种情况,速度和加速度由位置多项式求导得来。
在给出了起点的初始时刻、位置、速度、加速度和加加速度,终点要求的到达时刻、位置、速度、加速度和加加速度后,矩阵X,Y和T便完全已知了,于是便可以求出系数矩阵A和B的值,则多项式完全可求,轨迹规划完毕。
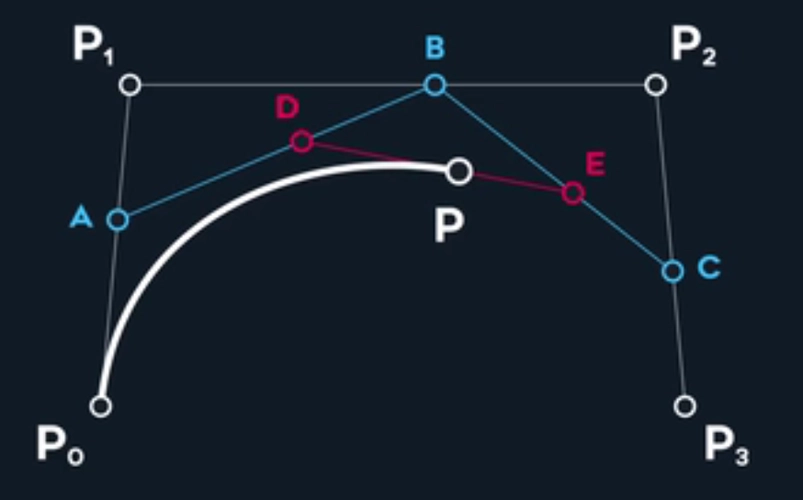
贝塞尔曲线法:
在自然界的车辆系统而言,规划的轨迹应该满足:轨迹连续,轨迹曲率连续;轨迹容易被车辆跟随,且容易生成。
继续推广以得到一般形式:
对于n+1个控制点而言,将会形成一条n阶贝赛尔曲线。对于三阶贝塞尔曲线而言,我们将有能力对其进行速度规划(一阶导数不为常数),对于四阶贝塞尔曲线而言,我们将有能力对其进行加速度规划(二阶导数不为常数),对于五阶贝塞尔曲线而言,我们将有能力对其进行加加速度规划(三阶导数不为常数)。如果我们给定了起点的初始时刻、位置、速度、加速度和加加速度,终点要求的到达时刻、位置、速度、加速度和加加速度。我们便可以根据贝赛尔曲线方程及其导数反解出所有的控制点。
由上式不难看出,当t=0时,∑项仅有P1-P0不等于0,即∑=P1-P0;当t=1时,∑项仅有Pn-Pn-1不等于0,即∑=Pn-Pn-1;故贝塞尔曲线起点和终点的切线方向即为特征多边形第一条边与最后一条边的方向。
怎么计算贝塞尔曲线长度的近似解?取delta_t为间隔的贝赛尔曲线上的若干个点,将这些点之间的矢量模相加得到。